| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- dijkstra algorithm
- 딕셔너리
- 백준
- Python
- 소수
- 투 포인터
- CCW 알고리즘
- Algorithm
- deque
- 외적
- 이진 탐색
- 너비우선탐색
- 다익스트라
- recursion
- binary search
- DP
- 에라토스테네스의 체
- 재귀
- BFS
- 알고리즘
- 에라토스테네스
- 비트연산
- 큐
- Bitmasking
- 위상정렬
- BOJ
- ccw
- CCW알고리즘
- 비트마스킹
- Two Pointers
- Today
- Total
꾸꾸리
[BOJ/Python] 17386_선분 교차1 본문
문제 출처:https://www.acmicpc.net/problem/17386
17386번: 선분 교차 1
첫째 줄에 L1의 양 끝 점 x1, y1, x2, y2가, 둘째 줄에 L2의 양 끝 점 x3, y3, x4, y4가 주어진다. 세 점이 일직선 위에 있는 경우는 없다.
www.acmicpc.net
문제
2차원 좌표 평면 위의 두 선분 L1, L2가 주어졌을 때, 두 선분이 교차하는지 아닌지 구해보자.
L1의 양 끝 점은 (x1, y1), (x2, y2), L2의 양 끝 점은 (x3, y3), (x4, y4)이다.
입력
첫째 줄에 L1의 양 끝 점 x1, y1, x2, y2가, 둘째 줄에 L2의 양 끝 점 x3, y3, x4, y4가 주어진다. 세 점이 일직선 위에 있는 경우는 없다.
출력
L1과 L2가 교차하면 1, 아니면 0을 출력한다.
제한
- -1,000,000 ≤ x1, y1, x2, y2, x3, y3, x4, y4 ≤ 1,000,000
- x1, y1, x2, y2, x3, y3, x4, y4는 정수
- 선분의 길이는 0보다 크다.
예제 입력 1
1 1 5 5
1 5 5 1예제 출력 1
1예제 입력 2
1 1 5 5
6 10 10 6예제 출력 2
0풀이
CCW 알고리즘을 이용하여 문제를 풀었다.
CCW 알고리즘에 대한 설명은 아래 게시물에 작성해두었다.
CCW(counter clockwise) 알고리즘
1. CCW 알고리즘 이란 점 A, B, C 세 점이 존재하였을 때, 이 세 점의 방향관계를 구하는 알고리즘이다. A, B, C를 연결하였을 때, 반시계 방향일 경우 양수를, 시계 방향일 경우 음수를, 직선일 경우 0
o773h.tistory.com
세 점이 일직선에 있는 경우는 없다고 하였으니 두 선분의 위치 관계는 다음과 같이 나타낼 수 있다.

첫 번째는 교차 하는 경우이고, 두 번째와 세 번째는 만나지 않는 경우이다.
CCW 알고리즘을 이용하게 되면 문제를 쉽게 풀 수 있다. 우선 첫 번째 교차하는 경우이다.

교차 하는 경우는 간단하다. 우선 한 선분의 한 끝 점을 기준으로 하여 자기 자신의 구한다. (그림에서 검은색 화살표)
이어서 다른 선분의 양 끝점을 향하는 벡터를 두 개 구한다. (그림에서 회색 화살표)
최종적으로 검은색 벡터와 회색 벡터 두개를 각각 외적하여 방향이 반대라면 교차함을 알 수 있다.
하지만 이 경우 한가지 문제가 생긴다. 그것은 바로 두 번째 만나지 않는 경우이다.

이 경우, 만나지 않지만 검은색 벡터를 기준으로 회색 벡터의 방향이 반대임을 알 수 있다. 이 경우는 반대로 생각하면 쉽게 해결할 수 있다.
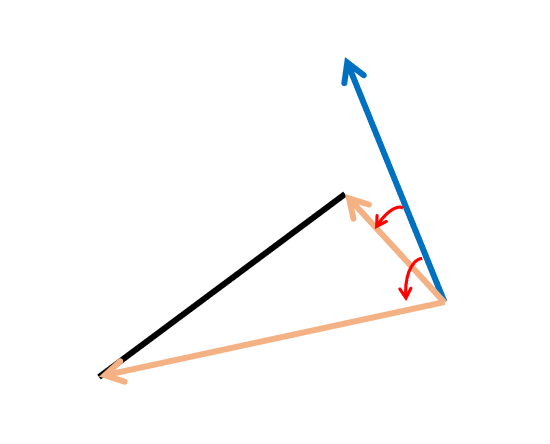
파란색 벡터를 기준으로 주황색 벡터를 구하게 되면, 방향이 모두 같음을 알 수 있다.
따라서, 두 선분이 만나지 않음을 구할 수 있다.

세 번째 경우는 어떤 선분을 기준으로 하여도 같은 방향임을 구할 수 있다.
따라서 위의 경우들을 통해 다음과 같은 결론을 내릴 수 있다.
- 두 선분을 각각 기준으로 하여 다른 선분의 양 끝점에 대한 벡터의 외적을 구하여 방향관계를 파악한다.
- 두 선분에 대하여 양 끝점에 대한 방향관계가 모두 반대라면 교차한다. (첫 번째 경우)
- 만약 한 선분에 대하여 양 끝 점에 대한 방향관계가 동일하다면 교차하지 않는다. (두 번째 경우)
- 마찬가지로 두 선분에 대하여 양 끝 점에 대한 방향관계가 동일하다면 교차하지 않는다. (세 번째 경우)
코드는 다음과 같다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
import sys
def ccw(pa,pb):
if pa[0]*pb[1] - pb[0] * pa[1]>0:
return -1
else:
return 1
x1,y1,x2,y2 = map(int,sys.stdin.readline().split())
x3,y3,x4,y4 = map(int,sys.stdin.readline().split())
p1 = (x2-x1,y2-y1)
p2 = (x3-x1,y3-y1)
p3 = (x4-x1,y4-y1)
p4 = (x4-x3,y4-y3)
p5 = (x1-x3,y1-y3)
p6 = (x2-x3,y2-y3)
if (ccw(p1,p2) * ccw(p1,p3))==-1 and (ccw(p4,p5) *ccw(p4,p6)) ==-1:
print(1)
else:
print(0)
|
cs |
- 입력받은 좌표를 통하여 벡터 p1(검은색 벡터), p2,p3(회색 벡터)를 생성한다.
- 마찬가지로 p4(파란색 벡터), p5,p6(주황색 벡터)를 생성한다.
- (p1,p2)에 대하여 ccw를 수행하고, (p1,p3)에 대하여 ccw를 수행한다.
- 두 번의 ccw를 수행하였을 때의 return 값이 반대이면(-1이라면) 교차할 가능성이 있다. (위 그림에서 두 번째의 경우도 있기 때문에 다른 선분 기준으로도 ccw를 수행해야 한다.)
- (p4,p5)에 대하여 ccw를 수행하고, (p4,p6)에 대하여도 수행하여 return 값이 반대인지 확인한다.
- 최종적으로 두 선분에 대하여 수행한 결과가 모두 반대 방향이라면 교차하므로 1을 출력하고, 아니면 0을 출력한다.
'Algorithm > BOJ' 카테고리의 다른 글
| [BOJ/Python] 17609_회문 (0) | 2023.01.19 |
|---|---|
| [BOJ/Python] 6439_교차 (0) | 2023.01.17 |
| [BOJ/Python] 2166_다각형의 면적 (4) | 2023.01.15 |
| [BOJ/Python] 11758_CCW (0) | 2023.01.14 |
| [BOJ/Python] 2589_보물섬 (0) | 2023.01.13 |



