| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 |
- DP
- Bitmasking
- Python
- 외적
- 다익스트라
- 너비우선탐색
- 비트연산
- 백준
- 소수
- dijkstra algorithm
- BFS
- Two Pointers
- CCW알고리즘
- 에라토스테네스
- deque
- Algorithm
- ccw
- 투 포인터
- CCW 알고리즘
- 재귀
- recursion
- BOJ
- 이진 탐색
- 에라토스테네스의 체
- 큐
- 알고리즘
- 비트마스킹
- binary search
- 위상정렬
- 딕셔너리
- Today
- Total
꾸꾸리
[BOJ/Python] 14567_선수과목 (Prerequisite) 본문
문제 출처:https://www.acmicpc.net/problem/14567
14567번: 선수과목 (Prerequisite)
3개의 과목이 있고, 2번 과목을 이수하기 위해서는 1번 과목을 이수해야 하고, 3번 과목을 이수하기 위해서는 2번 과목을 이수해야 한다.
www.acmicpc.net
문제
올해 Z대학 컴퓨터공학부에 새로 입학한 민욱이는 학부에 개설된 모든 전공과목을 듣고 졸업하려는 원대한 목표를 세웠다. 어떤 과목들은 선수과목이 있어 해당되는 모든 과목을 먼저 이수해야만 해당 과목을 이수할 수 있게 되어 있다. 공학인증을 포기할 수 없는 불쌍한 민욱이는 선수과목 조건을 반드시 지켜야만 한다. 민욱이는 선수과목 조건을 지킬 경우 각각의 전공과목을 언제 이수할 수 있는지 궁금해졌다. 계산을 편리하게 하기 위해 아래와 같이 조건을 간소화하여 계산하기로 하였다.
- 한 학기에 들을 수 있는 과목 수에는 제한이 없다.
- 모든 과목은 매 학기 항상 개설된다.
모든 과목에 대해 각 과목을 이수하려면 최소 몇 학기가 걸리는지 계산하는 프로그램을 작성하여라.
입력
첫 번째 줄에 과목의 수 N(1 ≤ N ≤ 1000)과 선수 조건의 수 M(0 ≤ M ≤ 500000)이 주어진다. 선수과목 조건은 M개의 줄에 걸쳐 한 줄에 정수 A B 형태로 주어진다. A번 과목이 B번 과목의 선수과목이다. A < B인 입력만 주어진다. (1 ≤ A < B ≤ N)
출력
1번 과목부터 N번 과목까지 차례대로 최소 몇 학기에 이수할 수 있는지를 한 줄에 공백으로 구분하여 출력한다.
예제 입력 1
3 2
2 3
1 2예제 출력 1
1 2 3예제 입력 2
6 4
1 2
1 3
2 5
4 5예제 출력 2
1 2 2 1 3 1힌트
3개의 과목이 있고, 2번 과목을 이수하기 위해서는 1번 과목을 이수해야 하고, 3번 과목을 이수하기 위해서는 2번 과목을 이수해야 한다.
풀이
위상정렬 문제이다. 과목들에는 순서가 정해져 있기 때문에 선수과목이 존재하는 과목의 경우, 선수과목을 이수하고 난 이후에야 이 과목을 수강할 수 있다.
예제 2에 대한 풀이는 다음과 같다.
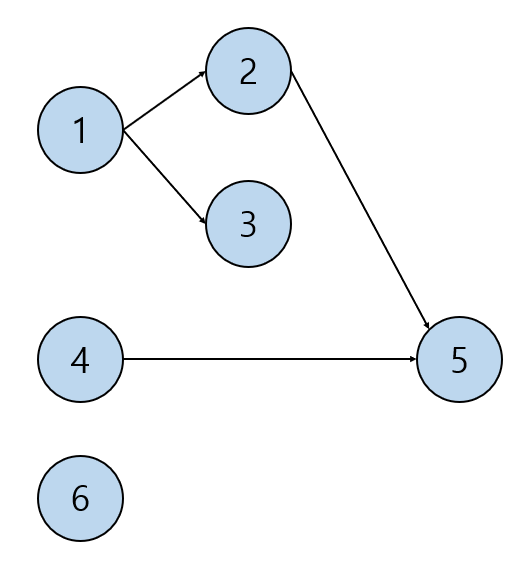
- 우선 주어진 간선 정보를 통한 그래프의 모양은 이렇게 생겼다.
- 여기서 1번 과목, 4번 과목, 6번 과목의 경우 들어오는 간선이 없으므로 진입차수가 0이다.
- 2번 과목과 3번 과목의 경우 1번 과목을 이수한 이후에 이수해야 하므로 진입차수가 1이다. (들어오는 간선이 1개이기 때문이다.)
- 5번 과목의 경우, 2번 과목과 4번 과목을 이수해야하므로 진입차수가 2이다. (들어오는 간선의 개수가 2개이다.)

- 우선 진입차수가 0인 과목들을 큐에 넣는다.
- 각 과목들마다 이수할 수 있는 학기 수를 구해야 하므로, 진입차수가 0인 과목들의 이수할 수 있는 학기수를 1로 설정한다.

- 큐에 들어있는 과목(노드)들을 하나씩 꺼낸다.
- 1을 꺼냈을 때, 1과 연결되어 있는 노드들의 진입차수를 1씩 줄인다.
- 여기서 2번 노드와 3번 노드의 경우, 각각 진입차수가 1이었지만, 이 과정을 통해 진입차수가 0이 된다.

- 이 과정을 통해 진입차수가 0이 된 2번 과목과 3번 과목 또한 큐에 넣어준다.
- 여기서 2번 과목과 3번 과목의 경우, 1번 과목을 이수한 이후에 이수할 수 있다.
- 그러므로 2번 과목과 3번 과목은 (1번 과목의 이수할 수 있는 학기 수) + 1 만큼의 학기 수가 필요하다.

- 이어서 큐에 있는 원소를 꺼낸다.
- 4번 노드를 꺼냈고, 4번 노드와 연결되어있는 5번 노드의 진입차수를 1 감소시킨다.
- 5번 노드의 경우, 진입차수가 2였지만, 1 감소되어서 1이 되었다. (2번 노드와 아직 연결되어있음을 의미한다.)

- 이어서 큐에 원소를 또 꺼낸다.
- 6번노드의 경우 연결되어있는 노드가 없다.

- 다음으로 큐에 원소를 꺼내면 2번 노드가 나오게 된다.
- 2번 노드의 경우 5번 노드와 연결되어있으므로 5번 노드의 진입차수를 1 감소시킨다.
- 이 과정을 통해 5번 노드의 진입차수가 0이 되었다.
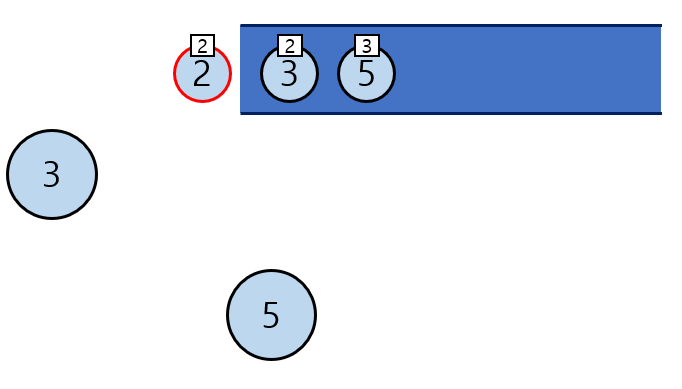
- 진입차수가 0이 된 5번 노드를 큐에 넣어준다.
- 5번 과목의 경우, 직전 과목인 2번 과목의 학기 수 + 1 만큼의 학기 수가 필요하다.
- 따라서 학기 수가 3이 된다.
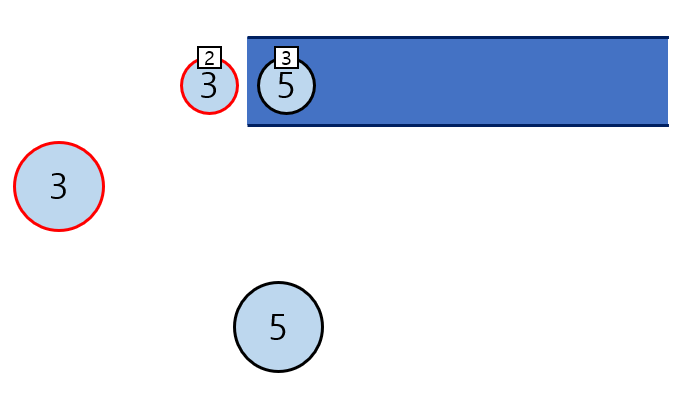
- 큐에 있는 원소를 꺼내고, 3번 노드는 연결된 노드가 없다.

- 마지막으로 5번 노드를 꺼내고 연결되어있는 노드가 없으므로 마친다.

- 큐가 비었으므로 종료한다.
코드는 다음과 같다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
import sys
import collections
def topological_sort(graph,indegree,result):
queue = collections.deque()
for i in range(1,n+1):
if indegree[i]==0:
queue.append(i)
result[i]=1
while queue:
node = queue.popleft()
for next in graph[node]:
indegree[next]-=1
if indegree[next]==0:
queue.append(next)
result[next] = result[node]+1
n,m = map(int,sys.stdin.readline().split())
graph = [[] for _ in range(n+1)]
indegree = [0 for _ in range(n+1)]
result = [0 for _ in range(n+1)]
for _ in range(m):
a,b = map(int,sys.stdin.readline().split())
graph[a].append(b)
indegree[b]+=1
topological_sort(graph,indegree,result)
print(*result[1:])
|
cs |
- graph는 각 과목(노드)들의 연결 상태를 저장한 리스트이다.
- indegree는 각 노드들의 진입차수를 저장한 리스트이다. a->b로 연결되어있다면, b의 indegree를 1 증가시킨다.
- result의 경우, 최종적으로 출력해야하는 각 과목을 이수하기 위하여 최소 몇 학기가 걸리는지에 대한 정보를 담는 리스트이다.
위상정렬의 과정은 다음과 같다.
- 진입차수가 0인 모든 노드를 큐에 넣는다. 그리고 해당 노드의 result값을 1로 설정한다.
- 큐에서 원소를 꺼내 해당 노드에서 나가는 간선을 그래프에서 제거한다. (목적지 노드의 진입차수를 1 감소시킨다.)
- 새롭게 진입차수가 0이 된 노드를 큐에 넣는다. 또한, 해당 노드의 result값을 직전노드의 값 + 1 로 설정한다.
- 2~3의 과정을 큐가 빌 때 까지 반복한다.
'Algorithm > BOJ' 카테고리의 다른 글
| [BOJ/Python] 7562_나이트의 이동 (0) | 2023.02.17 |
|---|---|
| [BOJ/Python] 2056_작업 (0) | 2023.02.16 |
| [BOJ/Python] 16562_친구비 (0) | 2023.02.14 |
| [BOJ/Python] 4485_녹색 옷 입은 애가 젤다지? (0) | 2023.02.13 |
| [BOJ/Python] 11779_최소비용 구하기 2 (0) | 2023.02.12 |



