| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- binary search
- Two Pointers
- BFS
- 소수
- 이진 탐색
- 투 포인터
- 다익스트라
- CCW 알고리즘
- Algorithm
- 알고리즘
- Python
- BOJ
- recursion
- 재귀
- 위상정렬
- Bitmasking
- 비트마스킹
- 딕셔너리
- DP
- ccw
- deque
- 비트연산
- 외적
- dijkstra algorithm
- CCW알고리즘
- 에라토스테네스
- 너비우선탐색
- 큐
- 에라토스테네스의 체
- 백준
- Today
- Total
꾸꾸리
[BOJ/Python] 10423_전기가 부족해 본문
문제 출처:https://www.acmicpc.net/problem/10423
10423번: 전기가 부족해
첫째 줄에는 도시의 개수 N(1 ≤ N ≤ 1,000)과 설치 가능한 케이블의 수 M(1 ≤ M ≤ 100,000)개, 발전소의 개수 K(1 ≤ K ≤ N)개가 주어진다. 둘째 줄에는 발전소가 설치된 도시의 번호가 주어진다. 셋째
www.acmicpc.net
문제
세계에서 GDP가 가장 높은 서강 나라는 소프트웨어와 하드웨어 기술이 모두 최고라서 IT강국이라 불리고, 2015년부터 세상에서 가장 살기 좋은 나라 1등으로 꼽히고 있다.
살기 좋은 나라 1등으로 꼽힌 이후 외국인 방문객들이 많아졌고, 그에 따라 전기 소비율이 증가하여 전기가 많이 부족한 상황이 되었다. 따라서 서강 나라의 대통령은 최근 개발이 완료된 YNY발전소 프로젝트를 진행 하기로 하였다. 발전소를 만들 때 중요한 것은 발전소 건물과 도시로 전기를 공급해 줄 케이블이다. 발전소는 이미 특정 도시에 건설되어 있고, 따라서 추가적으로 드는 비용은 케이블을 설치할 때 드는 비용이 전부이다. 이 프로젝트의 문제는 케이블을 설치할 때 드는 비용이 굉장히 크므로 이를 최소화해서 설치하여 모든 도시에 전기를 공급하는 것이다. 여러분은 N개의 도시가 있고 M개의 두 도시를 연결하는 케이블의 정보와 K개의 YNY발전소가 설치된 도시가 주어지면 케이블 설치 비용을 최소로 사용하여 모든 도시에 전기가 공급할 수 있도록 해결해야 한다. 중요한 점은 어느 한 도시가 두 개의 발전소에서 전기를 공급받으면 낭비가 되므로 케이블이 연결되어있는 도시에는 발전소가 반드시 하나만 존재해야 한다. 아래 Figure 1를 보자. 9개의 도시와 3 개의 YNY발전소(A,B,I)가 있고, 각각의 도시들을 연결할 때 드는 비용이 주어진다.
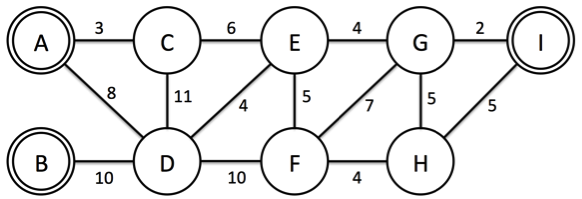
Figure 1
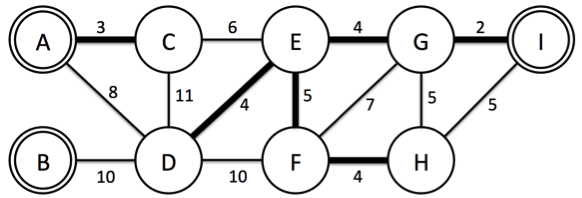
Figure 2
이 예제에서 모든 도시에 전기를 공급하기 위하여 설치할 케이블의 최소 비용은 22이고, Figure 2의 굵은 간선이 연결한 케이블이다. B 도시는 연결된 도시가 하나도 없지만, 발전소가 설치된 도시는 전기가 공급될 수 있기 때문에 상관없다.
입력
첫째 줄에는 도시의 개수 N(1 ≤ N ≤ 1,000)과 설치 가능한 케이블의 수 M(1 ≤ M ≤ 100,000)개, 발전소의 개수 K(1 ≤ K ≤ N)개가 주어진다. 둘째 줄에는 발전소가 설치된 도시의 번호가 주어진다. 셋째 줄부터 M개의 두 도시를 연결하는 케이블의 정보가 u, v, w로 주어진다. 이는 u도시와 v도시를 연결하는 케이블을 설치할 때 w의 비용이 드는 것을 의미한다. w는 10,000보다 작거나 같은 양의 정수이다.
출력
모든 도시에 전기를 공급할 수 있도록 케이블을 설치하는 데 드는 최소비용을 출력한다.
예제 입력 1
9 14 3
1 2 9
1 3 3
1 4 8
2 4 10
3 4 11
3 5 6
4 5 4
4 6 10
5 6 5
5 7 4
6 7 7
6 8 4
7 8 5
7 9 2
8 9 5예제 출력 1
22예제 입력 2
4 5 1
1
1 2 5
1 3 5
1 4 5
2 3 10
3 4 10예제 출력 2
15예제 입력 3
10 9 5
1 4 6 9 10
1 2 3
2 3 8
3 4 5
4 5 1
5 6 2
6 7 6
7 8 3
8 9 4
9 10 1예제 출력 3
16풀이
이 문제를 요약하자면 다음과 같다.
- 도시와 발전소가 존재한다. (노드)
- 도시는 케이블(간선)을 통하여 발전소와 연결되어야 한다.
- 다른 도시를 거쳐서 발전소와 연결되어도 된다.
- 도시는 발전소 한 군데와 연결되어야 한다. (두 군데 이상 연결되면 최소 비용이 될 수 없다.)
- 이때 사용되는 케이블의 최소비용을 구하는 문제이다.
얼핏보면 어려운 문제인 것 같지만, 아이디어만 떠올릴 수 있다면 쉽게 풀 수 있는 문제이다.
우선 도시를 기준으로 생각해보자.
도시는 다른 도시들을 거쳐서 최종적으로 발전소와 연결되어야 한다.
만약 발전소가 1개라면, 단순하게 최소 신장 트리를 구하는 문제임을 알 수 있다.
발전소를 기준으로 생각하게 되면 모든 발전소가 다른 도시들과 연결될 필요는 없다.

이 그림에서 B번 노드가 발전소이며, 다른 도시들과 연결되지 않은 상태임을 알 수 있다.
만약 다 순하게 최소신장트리를 이용하게 되면,
- A번 노드와 D번 노드가 연결된다.
- B번 노드와 D번 노드가 연결된다.
- 따라서 D번 노드는 발전소 세 군데와 연결돼있다. (D뿐만 아니라 C, E, F, G, H 또한 마찬가지이다.)
- 이는 도시가 한 군데의 발전소와 연결되어야 한다는 문제의 조건을 위반한다.
- 또한, 최소비용이 될 수 없다.
이 과정에서 문제가 생긴 이유는 이미 발전소와 연결되어 있는 도시가 다른 발전소와 연결됐기 때문이다.
따라서, 발전소와 연결된 도시가 다른 발전소와 연결되지만 않으면 문제를 쉽게 해결할 수 있다.
이 부분은 단순하게 발전소들을 하나의 집합으로 만들고 시작하면 된다.

최소신장트리를 구하기 위하여 크루스칼 알고리즘을 사용할 때, union-find를 이용하여 사이클이 생기지 않도록 한다.
발전소(A, B, I)를 하나의 집합으로 만들고 시작하게 되면, A와 D 혹은 B와 D를 연결할 때, 사이클이 생기므로 연결되지 않게 된다. 따라서 도시들은 모두 최소비용으로 발전소와 연결되게 된다.
코드는 다음과 같다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
|
import sys
def find_parent(parent,x):
if parent[x] != x:
parent[x] = find_parent(parent,parent[x])
return parent[x]
def union_parent(parent,a,b):
a = find_parent(parent,a)
b = find_parent(parent,b)
if a<b:
parent[b] = a
else:
parent[a] = b
n,m,k = map(int,sys.stdin.readline().split())
k_list = list(map(int,sys.stdin.readline().split()))
parent = [i for i in range(n+1)]
edges = []
if k>1:
for i in range(1,k):
union_parent(parent,k_list[0],k_list[i])
for _ in range(m):
u,v,w = map(int,sys.stdin.readline().split())
edges.append((w,u,v))
edges.sort()
result = 0
l = 0
for w,u,v in edges:
if find_parent(parent,u) != find_parent(parent,v):
union_parent(parent,u,v)
result += w
l+=1
if l==n-k:
break
print(result)
|
cs |
- k(발전소의 수)가 1이라면 단순하게 최소신장트리를 구하면 된다.
- 만약 k가 2 이상이라면, 발전소들을 하나의 집합으로 합친다.
- 최소신장트리를 구한다.
- 도시들만 (발전소 또는 발전소와 연결되어 있는 다른 도시)와 연결되므로 간선의 개수가 n-k(도시의 수)가 되면 break를 한다.
- 최종적으로 비용을 출력한다.
'Algorithm > BOJ' 카테고리의 다른 글
| [BOJ/Python] 1833_고속철도 설계하기 (0) | 2023.03.12 |
|---|---|
| [BOJ/Python] 18223_민준이와 마산 그리고 건우 (0) | 2023.03.11 |
| [BOJ/Python] 2637_장난감 조립 (0) | 2023.03.09 |
| [BOJ/Python] 2211_네트워크 복구 (1) | 2023.03.08 |
| [BOJ/Python] 1766_문제집 (1) | 2023.03.07 |


